Interference in 2-D
Interference in two dimensions is simply an extension of what occurs in one dimension. As waves overlap they will create many small regions of constructive and destructive interference over time.
Examine this video of interfering water waves.

The two sources of disturbance have the same frequency and because the medium is uniform, the wavelengths are identical.
Explanation of interference pattern
Regions in the video where the water is relatively calm are referred to as nodes – they are regions of destructive interference. Regions of crests  and troughs
and troughs  are referred to as antinodes – they are regions of constructive interference. Let us examine how all this works.
are referred to as antinodes – they are regions of constructive interference. Let us examine how all this works.
For convenience, the diagram below shows half the interference pattern created by the two vibrating sources.
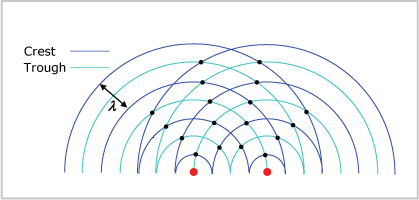
Regions of total destructive interference (nodes) are shown as dots. Notice the nodes are aligned, symmetrical and based on where troughs coincide with crests – the waves here are out of step.
The condition for destructive interference is related to the wavelength of the waves and the distance of the node from the two sources. Node A is two wavelengths in distance (L1) from one source and two and one-half wavelengths (L2) from the other, as shown below.
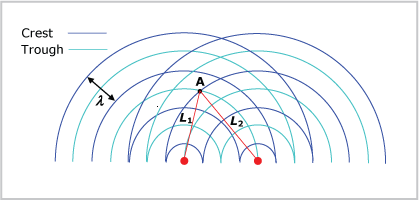
For node A, the path difference is one-half a wavelength (2.5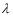 -2.0
-2.0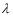 ). Other nodes occur where the path difference is 1.5
). Other nodes occur where the path difference is 1.5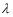 , 2.5
, 2.5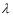 , 3.5
, 3.5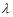 and so on. The condition for any node is that the path difference must always be one-half of a wavelength or an odd number multiple of one-half a wavelength.
and so on. The condition for any node is that the path difference must always be one-half of a wavelength or an odd number multiple of one-half a wavelength.
The internodal distance |L2 – L1| = (n-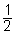 )
)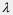 , where n = 1, 2, 3 ...
, where n = 1, 2, 3 ...
The condition for all antinodes is that the path difference |L1 – L2| must be equal to zero or a whole number, multiple wavelength because the waves must be in step.
The path difference |L2 – L1| = n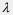 , where n = 0, 1, 2 ...
, where n = 0, 1, 2 ...

Two loudspeakers X and Y are part of a public entertainment sound system (see diagram below). For a while they emit a continuous sound of wavelength 0.60 m. A girl walks from point A to point I noting that the sound alternates in loudness from soft (B, D, F and H) to loud (A, C, E, G and I). Note that line OE perpendicularly bisects line XY.

a) What is the path difference in the sounds from the two speakers to the point F?
b) If XA is equal to 12.9 m what is the distance YA?
c) Is the distance between each point from A to I identical? Explain.

a) Point F is the first node (sound is soft) from point E. This means the path difference is one-half of a wavelength. Since 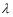 = 0.60 m, the path difference is 0.30 m.
= 0.60 m, the path difference is 0.30 m.
b) Point A is a position of total constructive interference (sound is loud). From the diagram it can be deduced that this must be the second loud region from point E.
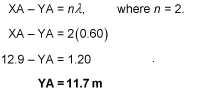
c) The distances are not identical. The nodes and antinodes lay on arcs not radial lines.

Interference
1 |
State whether the following statements are true or false.Constructive interference only occurs with waves of the same amplitude. |
2 |
Troughs are regions of destructive interference. |
3 |
Destructive interference only occurs where the path difference between wave sources is one-half a wavelength. |
4 |
Antinodes are regions where the path difference between wave sources is one wavelength or a multiple of a wavelength. |





