Mechanical waves

Consider the string/wire of a guitar, violin or cello. When the tensioned string or wire is plucked by finger or set into oscillation by a bow, the initial travelling wave is reflected at a fixed end. The initial and reflected travelling waves interfere, and if the wavelength and string length are appropriate, a standing wave will form. Unlike the ideal case, some energy is transferred from the standing wave to the sounding board of the instrument, which if carefully crafted, will amplify the sound because of resonance.

The possible frequencies of an oscillating string can be understood as a set of standing waves. The most simple, transverse standing wave pattern is shown below.

There are two nodes (N), one at each fixed end and one antinode (A) at the centre. If the length of the string (L) is not greatly altered when stretched, the standing wave wavelength is = 2L or f₁ = v/(2L). This frequency is referred to as the fundamental frequency and is the lowest standing wave frequency for this length of string/wire for the supplied tension and string/wire mass.

If the string is plucked or bowed at some other point, it is possible to create a standing wave with three nodes (one at each end and one in the middle) and two antinodes between the nodes. In this case the wavelength is = L or f₂ = v/L.

You will notice that f₂ is twice f₁. It is possible to create other standing wave patterns and when their frequencies are compared to f₁, there is always a whole number relationship.

The higher frequencies (f₂, f₃,...) are referred to as overtones. All the frequencies (f₁, f₂, f₃, ...) are also called harmonics.

A flute is a pipe that effectively has two open ends, one at the mouthpiece and the other at one end of the instrument. A flautist blows into the mouthpiece and sets a travelling wave moving along the pipe to the open end where it becomes a 180° out-of-step, reflected wave. The waves interfere and if the effective length of the air column (decided by the flautist's finger placement over holes in the pipe) is 'just right', a standing wave is established.

The most simple longitudinal standing wave pattern is shown below.

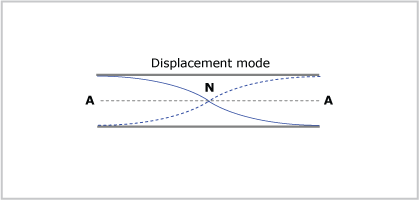
It looks like a transverse wave but represents the horizontal amplitude of air particles from their mean positions, rotated 90°.

The same standing wave can be described in terms of maximum sound pressure (see below) rather than displacement of the air particles as shown above. Both views are correct but result in very different diagrams. You need to be clear as to the context in which you are describing the standing wave.

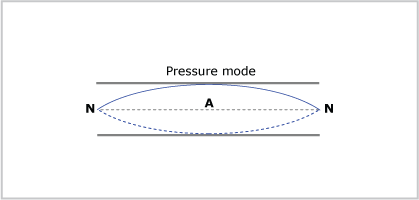
In either case, if the length of the air column is L, the standing wave wavelength is 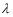= 2L or f₁ = v/(2L).

The standing wave with the closest frequency to the fundamental occurs when 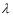= L or f₂ = v/L. As is the case with stringed instruments, there exists a whole number relationship between the harmonics.

A clarinet, like all reed instruments, can be thought of as a pipe with one open end and one closed end (the reed end). The standing waves are different to an open pipe.

The most simple longitudinal standing wave pattern is shown below.

If the length of the air column is L, the standing wave wavelength is 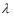= 4L or f₁ = v/(4L). The standing wave with the closest frequency to the fundamental occurs when 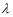= 4L/3 or f₂ = 3v/(4L). The harmonic frequencies are an odd whole number multiple of the fundamental frequency.